Experiments in Psycho-Acoustics
Updated Sept. 18, 2001
Time Domain Banner

Does the ear and brain mix signals? If so, what is the non- linearity that this implies? And if there is non-linearity in our hearing, why can we still discern unique sounds within a large ensemble? Wouldn't mixing turn our experience of music into a distorted mess?

If on the other hand there is no mixing involved, only summing, how can we perceive "beat frequencies"? Furthermore, how could we possibly perceive "phantom notes" above and below actual sounds if there is no non-linear mixing involved in the process of perceiving sound?

Here is your opportunity to explore this fascinating aspect of human hearing, perhaps even answering some of these questions for yourself. Keep your ears - and your mind - open while you do these experiments.

Note: If your sound card has digital processing options such as reverb, chorus, or (especially) "3D-wide", be sure to disable them for these experiments. They can interfere with proper operation, especially of the binaural (stereo) samples.

Part 1: It's All In The Mix

Let's start by listening once more to individual, pure sine waves. The first is A=440, and the second is a perfect fifth above that (E=660). Both are monaural, so the sound should appear to be sounding right in the middle of your head, or perhaps directly in front or behind you.

MP3 clip A = 440 Hz. Sine Wave
MP3 clip E = 660 Hz. Sine Wave
Stereo Summing: The first summing experiment we'll listen to is what we might call "stereo summing". The first tone (A=440) is applied to the left channel, and the second tone (E=660) to the right channel. You will have no difficulty hearing each tone individually. However, you also should have no trouble perceiving the two notes as a musical interval, or two-note "chord". In this rather limited sense, your brain is summing the two notes, arriving by separate channels into each brain hemisphere. However, the last experiment in this series will demonstrate that the brain actually does not implement summing of a fully binaural pair of frequencies.
MP3 clip Stereo summing 440/660 Hz.
Incidentally, this file is good for checking your stereo separation. In some of the experiments that follow, a reasonably good approximation of true binaural (independent left and right channels) is necessary for best results. Listen to just one earphone at a time (cover the other one with your hand), you should hear only one tone in each 'phone, with very little bleed.
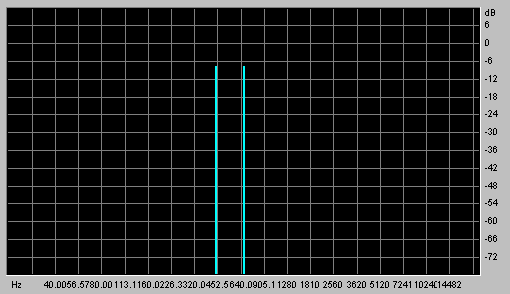
Monaural (true) Summing: Now let's sum the two tones into a single monaural signal (left and right channels identical). Acoustically, we've just summed the two tones; as the frequency domain graph below demonstrates, it contains only the two frequencies A=440 and E=660. However, this is where the "psycho-" in psycho-acoustics comes into play.
MP3 clip Mono summing 440/660 Hz.
Spectrogram, 440 + 660 Hz. summed

Speaking for myself, there are times when I hear two distinct tones, much as in the case of the stereo summing experiment. Other times the lower tone appears to predominate, with the higher tone only adding "colour" or timbre to the sound. After looping a number of times, the higher tone may "disappear" completely, leaving only the lower tone with a somewhat harsher, almost bassoon-like quality. This is not surprising, since the higher tone is harmonically related (albeit indirectly) to the lower tone. The brain appears to synthesise the higher octave of the E=660 tone (1320 Hz), then chooses to perceive it as the third harmonic of the fundamental tone.

On rare occasions, it seems that a lower octave at A=220 is also present. If this occurs for you, it demonstrates the illusion of "phantom bass". This effect can also be noticed when listening to stereo sets with small speakers incapable of reproducing low bass. The ear will quite often "fill in" the missing frequencies, making it appear that the little speakers are doing a better job than they actually are.

One phenomenon I have not observed, either in stereo or monaural mixing, is "psycho-synthesis" of frequencies other than the octave. For instance, no matter how many times I listen to the summed 440 + 660 Hz. clip, I never "hear" the sum of the two frequencies, i.e. 1100 Hz. which would approximately be the C-sharp an octave above middle C. In other words, the sound never has an identifiably "major" tonality to it, sounding always like a completely neutral perfect fifth interval. (If you're wondering what I'm on about, the next experiment will hopefully clarify.)
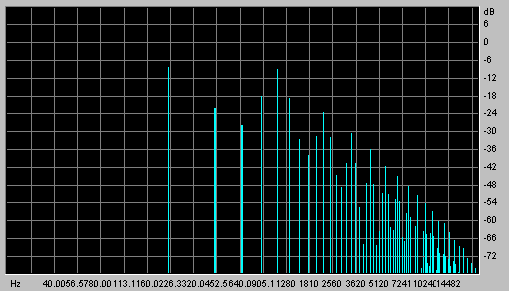
Mixing: This time we'll actually mix the two signals by applying a non-linearity. The function used was an "RMS filter", which essentially squares each point on the summed signal. The result is in the sound clip below, along with its spectrogram. The two original frequencies are shown in bold lines, note that there is now a lower tonic (difference frequency) at A=220 Hz. as well as sum frequencies every 220 Hz. above that.
MP3 clip Mono mixing 440/660 Hz.
Spectrogram, 440 + 660 Hz. mixed

Now the higher (660 Hz) tone has apparently disappeared completely, being absorbed in the wash of harmonics created by the mixing process. To my ear it now just sounds somewhat like a kazoo or maybe an oboe on steroids.

However, for me the sound now has a distinctly "major" tonality, because of the presence of the sums which add the major third to the fundamental and perfect fifth tones. If you can't quite hear what I'm talking about, here is the same sound except that I've applied a sharp low-pass filter, with a cut-off frequency just above 1100 Hz., and emphasized the difference signal (A=220) and perfect fifth (E=880):
MP3 clip Mixed and filtered
Spectrogram, mixed and filtered

Phantom Notes: Now for a demonstration, and one possible explanation, for the phenomenon known as "phantom notes". It has been reported, especially by woodwind players, that two instruments playing different pitches together can result in an unrelated, but clearly audible higher note. The usual interpretation is that the phantom note represents the sum of the frequencies of the two "real" notes. I don't believe that this is correct, however, based on the summing experiments shown at the beginning of this section. I have not succeeded in perceiving any semblance of phantom notes by summing pure sine waves, if you do I'd be interested in hearing from you.

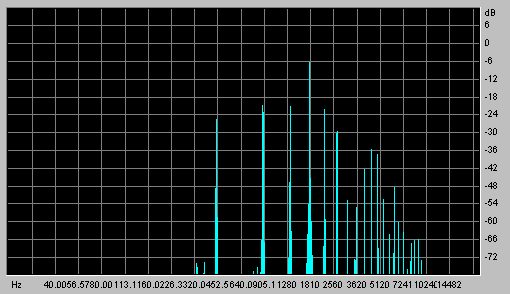
Rather, I suspect that what is happening is that "shared harmonics", to coin a term, are responsible for the phantom notes effect. Let's say that we have a sound with its fundamental at A=440, and a strong 9th harmonic content (9 * 440 = 3960 Hz., which is close to a major 16th, or an octave higher than a major 9th). Now let's take a second note at E=660, and assume that it has a prominent 6th harmonic (a perfect fifth an octave up). This would calculate out to (660 * 6) = 3960 again. In such a case, the two different harmonics could augment each other, particularly if stereo imaging were involved.

Here's a demonstration. As it turns out, the "oboe" sound from my Yamaha XG synth suits the above requirements (strong 6th and 9th harmonics) very well. Let's see if we can hear a phantom high B when an A=440 and E=660 are played together. First, the two notes separately. The spectrogram of the A=440 sound is also shown below.
MP3 clip Oboe sound, A=440 mono
MP3 clip Oboe sound, E=660 mono
Spectrogram, Oboe A=440 sound

If you have a good ear, you might be able to pick out the 9th harmonic (high B) in the A=440 sound. However, it's unlikely that you'll hear it in the E=660 sound, because of the perfect fifth's tendency to "hide" in the fundamental, as in the mono summing example given earlier.

Incidentally, there is another illusion at work here. Because of the extremely strong second and fourth harmonics in this sound, it can appear that the fundamental frequency is an octave, or even two octaves higher than it really is. Compare with the pure sine wave sounds at the beginning of this piece, and I'm sure you'll see what I mean.

Finally, listen to both notes played together. The A=440 sound is placed somewhat left of center in the stereo image, and the E=660 sound is panned to the right. Do you hear that high B dead-center in the stereo field? That's the phantom note!
MP3 clip Phantom note demonstration
Beat Frequencies: Finally, there is the phenomenon of "beat frequencies" which is often explained as a psycho-acoustic mixing process. The reality of beat frequency perception is undeniable, as this experiment will demonstrate. Again, however, I believe that this phenomenon can be explained without the necessity to postulate non-linearity (mixing) in our perception of sound.

Thus far we have only experimented with sounds whose difference frequency (also known as beat frequency) is quite high. What if the difference between the two frequencies is very slight, resulting in a difference (beat) frequency of only a few Hertz? The two sound bites below are 440 Hz. and 443 Hz.; this represents a difference in pitch of about 12 cents, if you listen to the samples a few times in succession I'm quite sure you'll hear the slight pitch difference.
MP3 clip 440 Hz. sine wave, mono
MP3 clip 443 Hz. sine wave, mono
Now listen to the two tones, summed together into a mono signal. You will have no trouble discerning the beat frequency.
MP3 clip 440 Hz. + 443 Hz., mono
So what's going on here? Are the ear and brain using nonlinear mixing to perceive the 3 Hz. difference frequency? I would say no. For an alternate explanation, let's first have a look at what the waveform looks like in the time domain:

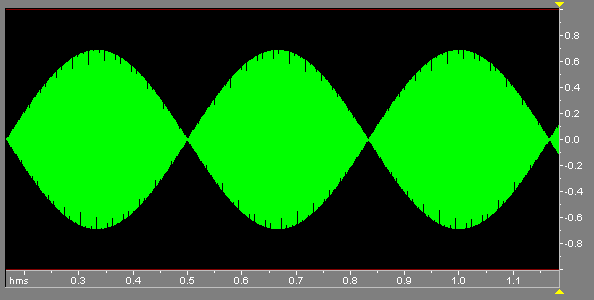
440/443 Hz. summed, showing beat envelope

If you don't quite understand what's going on here, have a look at an "expanded" version below; this is what the wave would look like if the summed frequencies were 50 Hz. and 53 Hz.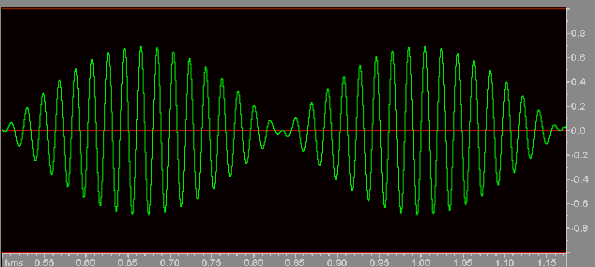

50/53 Hz. summed, showing beat envelope

Note that the wave has a distinct "envelope", or repetitive wave-like fluctuation in peak amplitude. In a sense it therefore behaves as a single tone frequency, modulated by the 3 Hz. envelope. What I believe is happening is that the ear perceives that single tone in the frequency domain as always, but perceives the envelope in the time domain.

This theory is borne out by the observation that as the difference between the two signals increases, the beat of course gets faster and faster, ending up in with a sort of "warbling" quality. At a certain point corresponding to about a quarter of a semitone, the sound morphs from the single modulated tone into two discrete, out-of-tune notes. At no point does the ear perceive a low bass frequency. A sample is provided below; this is A=1760 summed with 1860 Hz. You'll probably be able to hear it as a single tone modulated by 100 Hz., or as two dissonant tones. However, no matter how you try, you probably won't be able to perceive a discrete 100 Hz. (low bass) note. My conclusion is that, while there are definite illusions relating to hearing, they are not caused by non-linear response in the ear, nervous system or brain.
MP3 clip A=1760 + 1860 Hz., mono
We'll end off this little series of experiments with the one that I personally find the most surprising. You'll definitely need headphones for this one, as it is a binaural experiment. As before, we use A=440 Hz. and 443 Hz., except that this time each frequency is isolated in its own channel; 440 Hz. in the left ear, and 443 Hz. in the right ear.
MP3 clip A=440 + 443 Hz., binaural
The amazing result is that you will hear very little, if any "beating". Instead, you'll hear two discrete and slightly out-of-tune notes, or you may perceive it as a single tone "smeared out" across the stereo field. Any residual warble you perceive is most likely due to imperfect stereo separation in the process from my sound card, through the mp3 encoding process, and through the decoding process via the sound card on your end.

This indicates to me that the brain does not even do any summing, let alone nonlinear mixing, on purely binaural signals (input to the left ear completely independent of input to the right ear). As a practical side-note, if you use the beating effect to tune instruments to each other, you will hear a more distinct beat if both instruments are close together directly in front of you (simulating a mono signal) than if they were positioned directly to the right and left of you (approximating a binaural signal).

However, in psycho-anything there are no absolutes, and psycho- acoustics is no exception. In the next article we'll explore the fascinating possibility of Brain-wave synchronisation, in which we use binaural beats (the ones we can't hear!) to perhaps influence our brain wave frequency, and thereby state of mind. Or perhaps not... either way, it should be interesting. Stay tuned!

Fred Nachbaur
 
Addendum: Phantom Bass revisited Andrew Purdam pointed out that the phantom bass phenomenon has been known to organists since the 17th century. Clifford N. Bohnson [Past Dean, Ocean County (NJ) Chapter, American Guild of Organists] writes further:

"As an organist and one who has helped build and voice a goodly number of organs, I can attest to the fact that the sub- difference tone is alive and well in contemporary organ-building. Using a 16' note with a properly-tuned fifth above, you create a "resultant" which sounds very distinctly an octave below the 16' note. This "stop" on an organ is labelled "32' Resultant". It has a further interesting property in that, if reasonably soft-sounding stops are used, the 32' tone is very usable under soft manual stops, whereas the same "resultant" can fill in even under a quite full organ sound.

"I have played three organs within the past two years that have very effective "resultants" here in the New Jersey area.

Another highly interesting reference is Acoustic bass of pipe organ. The author reaches essentially the same conclusion that I do, that there is not any nonlinear mixing, but that the reality of the phantom bass cannot be contested. Interestingly, he also relates the phenomenon to the ear's tendency to fill in the tonic of a chord even if it is not present.

So, alright then. Can we demonstrate an organ "resultant" in the electronic medium? Here's an mp3 of - again - my XG synth's imitation of a pipe organ diapason. About two seconds of a low C are played (lowest frequency is about 65.5 Hz, i.e. 16' pipe range), then the G above it is played. Can you hear a 32' pipe (very low C sound)? In case you're interested, the NoteWorthy Composer source file is available here.

MP3 clip Organ diapason sound, mono

Just for reference (and for the fun of it) here is a sonogram of this sound. A sonogram is another way to plot sounds in the frequency domain, with the added advantage that they are usable with non-steady-state sounds. In other works, a sonogram shows changes in a sound as it plays out, and can therefore be viewed as a kind of "voice-print". Time is plotted horizontally, and frequency is shown vertically. The color indicates the intensity of that frequency component at any given time.

As you see in the sonogram, there is not even a hint of any lower octave as the perfect fifth starts playing. Verification once again that what you hear (if you hear it) is your marvellous human brain at work, and is not a "physical" phenomenon.

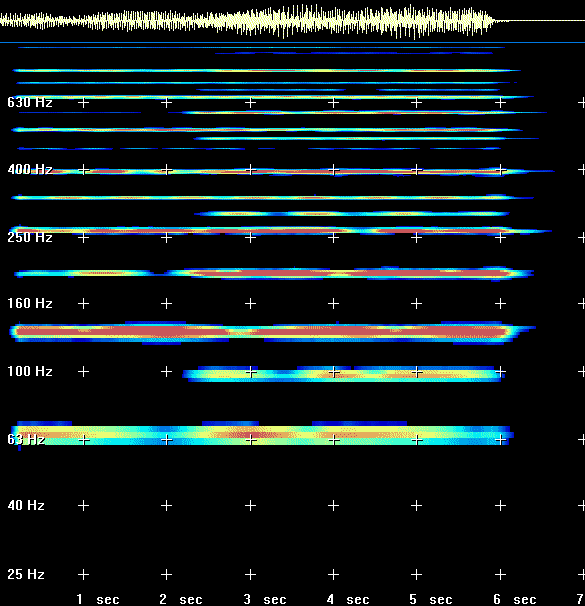
Sonogram of organ sound

Back to Fred's Freebies

Other interesting sites on Psycho-Acoustics:
Nakajima-Lab: Auditory Illusions and Tricks
Scientific American: Analysis: Dissecting the Brain with Sounds

Dogstar Music Banner
To Dogstar Music's Home