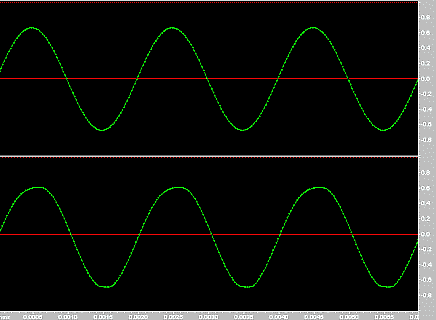
Time-domain graph at 1-watt output, 8 ohms
|
Part 1: Introduction |
Part 2: How It Works |
Part 3: Performance |
Part 4: Construction |
Part 5: Parts List |
Part 6: Sound Sample |
| PARAMETER | SPECIFICATION | NOTES |
| Max. Output power (8 ohms) | 1 watt | before onset of clipping |
| Max. Output power (4 ohms) | 1.15 watt | before onset of clipping |
| Effective Output Resistance | 6.6 ohms | measured at full output |
| Input Resistance | 100 kilohm | determined by volume control R6 |
| Input Sensitivity | 0.9 volts RMS | min. input signal for full output |
| Low Frequency Response | -3 dB @ 40 Hz. | (-6 dB @ 25 Hz.) |
| High Frequency Response | -3 dB @ 9 kHz. | (-6 dB at 15 kHz.) |
| Maximum THD | 6.74% | calculated at full output |
| Typical THD | 2.52% | calculated at 1/2-voltage point |
| Hum and Noise | < -63 dB | relative to maximum output |

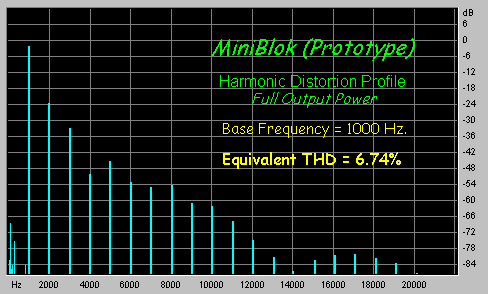
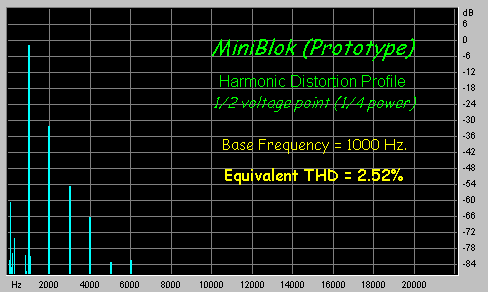
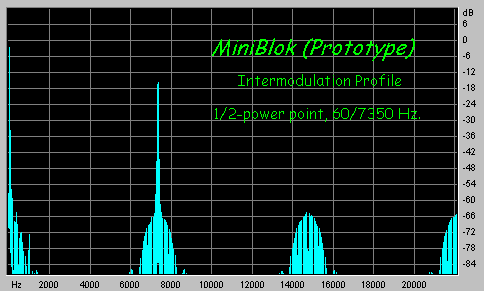
 |
 |
 |
BACK | INDEX | NEXT |
 |
 |
 |
BACK | INDEX | NEXT |